PLC Programming HandbooksPopular ArticlesNavigationUser login |
Getting the Point about Floating Point NumbersThe Freedom of Floating PointFloating point numbers (also known as 'real numbers') give a certain freedom in being able to represent both very large and very small numbers in the confines of a 32 bit word (that's a double word in our PLCs). Up until this point the range of numbers we were able to represent with a double word would be from 0 to 4,294,967,295. Floating point on the other hand allows a representation of 0.0000000000000001 as well as +/-1,000,000,000,000. It allows for such large numbers that we can even keep track of the US national debt. Floating point gives us an easy way to deal with fractions. Before, a word could only represent an integer, that is, a whole number. We'd have to use some tricks to maybe imply a decimal point. For instance, a number like 2300 in a word could be taken to represent 23.00 if the decimal point is "implied" to be in the 1/100th place. This might be all we need but it can get a bit tricky when it comes to math where we want to retain a remainder. The trick is to get some sort of format where the decimal point can "float" around the number. Real Numbers in the Real World
At this point let's deal with an example. In this case we're using an Automation Direct DL250 PLC which conveniently has the ability to handle real numbers (floating point). Our PLC is reading a pressure transducer input whose max reading is 250 psi. In our PLC the max number is represented by 4095 (FFF in hex). So essentially to get our real world reading we would need to divide 4095 by 16.38 (4095 reading / 250 max pressure). This is easily done with real numbers but our reading is in decimal. So the BTOR instruction is used to convert the decimal number to a real number format. Then we use the special DIVR instruction to divide it with a real number and get our reading. The resulting ladder logic would look like below.
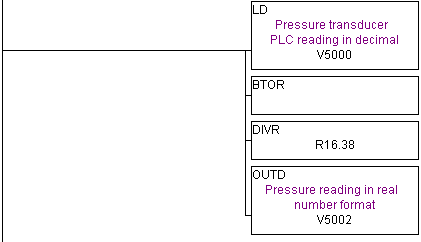 If you're a complete newbie at this and don't understand the ladder logic then don't worry about that. We'll get into ladder latter. Just understand that when you need to deal in fractions you'll most likely want to turn to real number formats in the PLC instruction set. If you're still staying afloat in all these concepts and want to understand more then read on...
Sinking Deeper into Floating Point Numbers
Floating point is basically a representation of scientific notation. Oh yeah? What's scientific notation? Scientific notation represents numbers as a base number and an exponent. For example, 123.456 would be 1.23456 x 102. That 10 with a little 2 above is telling us to move the decimal two spaces to the right to get the real number. Another example, 0.0123 would be 1.23 x 10-2. That little -2 indicates we move the decimal point in the opposite direction to the left. (Just a heads up, in the PLC you may be able to use scientific notation but in a different form like 1.23456E2 which is the same as a first example.) The number 10 here means we're dealing in decimal. We could just as easily do scientific notation in hexadecimal (123.ABC x 162) or even binary ( 1.0101 x 22, this binary one becomes important later on). The FormatAt some point in history a bunch of geeks got together and agreed upon a certain format or layout for a 32-bit floating point number. Due to a lack of originality, it officially became called "IEEE Standard 754". Here it is in all it's glory.
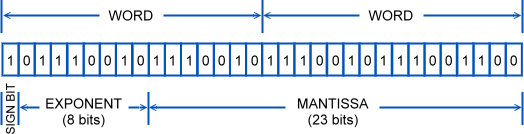 First there is the sign bit. It doesn't get any easier then this. If the bit is 0 then the number is positive but if it is a 1 then it is negative. Flip the bit and you change the sign of the number. What power.
The exponent is the same as our little number above the 10 in scientific notation. It tells us which way the decimal should go so it needs to be positive (go to the right) or negative (go to the left). Here we are again trying to deal with negative numbers but in this case the geeks decided to use what's called a bias or offset of 127. Basically this means that at a value of 127 the exponent is 0. Any number below 127 will cause a negative exponent. Any number above 127 will be a positive exponent. So a stored value of 200 indicates an exponent of 73 (200-127). The mantissa (or significand, if that is any easier to say) represent the precision bits of the number. In our example above it was the 1.23456 part of the scientific notation. The final nomenclature in scientific notation would be: (sign) mantissa x baseexponent Normally the base would be 10 but in this case it will be 2 since we are only dealing in binary. Since it's in base 2 (or binary) there's a little optimization trick that can be done to save one bit. Waste not, want not, you know. The trick comes about by realizing that scientific notation allows us to write numbers in many different way. Consider how the number five can be 5.00 x 100 0.05 x 102 5000 x 10-3 These are all the same number. Floating point numbers are typically in a normalized form with one digit to the left of the decimal (i.e. 5.00 x 100 or 4.0 x 103). The exponent is always adjusted to make this happen. In terms of using binary we'll always have a 1 in front (i.e. 1.0 x 23). You wouldn't have 0.1 x 24 as it wouldn't be normalized. So in this case it's always safe to assume that the leading digit is a 1 and therefore we don't have to store it. That makes the mantissa actually 24 bits long when all we have are 23 bits of storage. Ah, what we do to save one bit. WARNING: It's Not a Perfect WorldWith all this power using floating point you are probably thinking, "I'll just use it all the time". There's a problem though as this method can actually lose some precision. In many cases it will be negligible and therefore well worth it to use real numbers. In other cases though it could cause significant errors. So beware. Consider what would happen if the mantissa part of the floating point format was actually longer then 24 bits? Something has to give and what happens is the end is truncated, that is, it is cut off the end and lost. Here's an example of a 32-bit number 11110000 11001100 10101010 00001111 which would be 4039944719 in decimal In floating point with only 24 bits it would have to be 1.1110000 11001100 10101010 x 231 which when coverted back would be 11110000 11001100 10101010 00000000 and therefore 4039944704 in decimal. That's a difference of 15. During normal math this might not be of concern but if you are accumulating and totalizing values then that kind of error could really make the bean counters mad. This is simply a case of knowing your limitations. Glutton for Punishment: Further ReadingThere's more on this subject concerning things like double precision, overflow, zero and 'not a number' which you can read about in these excellent articles. What Every Computer Scientist Should Know About Floating-Point Arithmetic IEEE Standard 754Floating Point Numbers Introduction to Floating point calculations and IEEE 754 standard |

